Объем правильной четырехугольной пирамиды со стороной 4 и ребром √17

Задание

Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 4, а боковое ребро √17

Решение

1. Объем правильной четырехугольной пирамиды равен 1/3 произведения площади квадрата, являющегося основанием пирамиды S на высоту h:
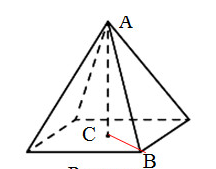
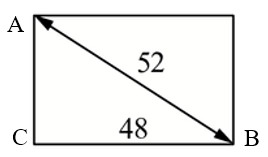
   V=1/3*h*S_осн=1/3*h*a²
2. Сторона основания известна. Найдем высоту пирамиды. Для этого рассмотрим треугольник ABC. Треугольник ABC — прямоугольный (угол C — прямой).
   CB = 0,5*d, где d — диагональ квадрата (основания пирамиды).
   d = √2*a, где a — сторона квадрата (сторона основания).
   Тогда CB = 0,5*√2*a = 0,5*√2*4 = 2√2
3. Высоту CA найдем по теореме Пифагора:
   AC²=AB²-CB² = (√17)²-(2√2)² = 17-8 = 9
   AC=3
4. Осталось найти объем пирамиды:
   V=1/3*h*a² = 1/3*AC*a² = 1/3*3*4² = 1*16 = 16

Ответ: 16