В треугольнике ABC ∠C=90°, CH—высота, BC=16, sinA=0,25

Задание

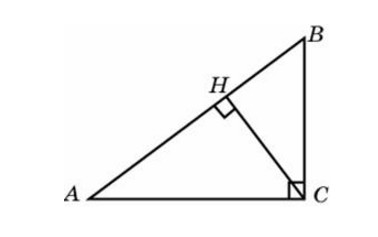
В треугольнике ABC угол C равен 90°, CH—высота, BC=16, sinA=0,25. Найдите длину отрезка BH.

Решение

1. Мы знаем, что синус угла – это отношение противолежащего катета к гипотенузе. Исходя из этого определения найдем гипотенузу АВ:
   sinA=СВ/АВ
   0,25=16/АВ
   АВ=16/0,25=64
2. Треугольники АСВ и СНВ подобны по двум углам (угол С = угол Н, по условию; угол В – общий). Из подобия треугольников следует:
   СВ/АВ=НВ/СВ
   16/64=НВ/16
   НВ=16*16/64=4

Ответ: 4