Задание
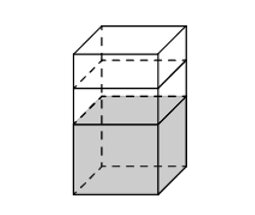
В бак, имеющий форму правильной четырехугольной прямой призмы со стороной основания, равной 30 см, налита жидкость. Чтобы измерить объем детали сложной формы, её полностью погружают в эту жидкость. Найдите объем детали, если после её погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.
Решение
- Для решения данной задачи необходимо знать формулу для нахождения объема прямой призмы:
Объем прямой призмы равен произведению её высоты на площадь основания:
V=h*Sоснгде V — объем призмы, S — площадь основания, h — высота призмы.
- Найдем площадь основания призмы:
S = 30*30 = 900 см2
Высота призмы равна разнице уровней жидкости до и после погружения детали: h = 10 см.
- Теперь мы можем вычислить объем детали:
V = h*Sосн = 10*900 = 9000 см3
Объем детали составляет 9000 кубических сантиметров.
Ответ: 9000

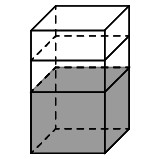

Откуда взялось 10
Добавили пояснение в текст решения задачи. 10 см — это высота призмы, которая равна разнице уровней жидкости до и после погружения детали (из условия задачи).