Задание
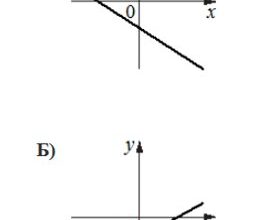
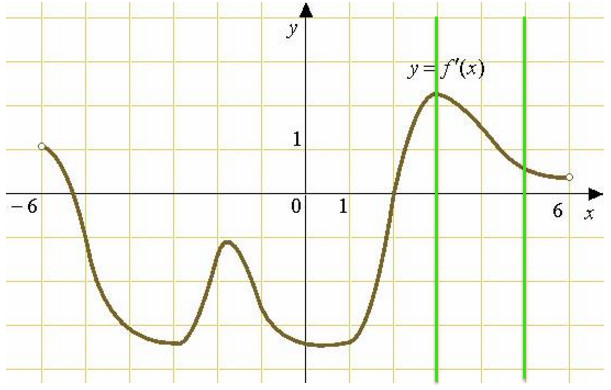
На рисунке изображён график y=f'(x) производной функции f(x), определенной на интервале (-9;8). В какой точке отрезка [1;7] функция f(x) принимает наименьшее значение?
Решение
- Обратим внимание на то, что на рисунке изображен график производной функции.
- Покажем рабочий интервал [1;7]вертикальными зелеными линиями.
- На данном интервале производная функции положительна.
- Мы знаем, что если производная функции положительна, то функция возрастает.
- На основе выше сказанного делаем вывод, что функция на интервале [1;7] возрастает, а это говорит о том, что наименьшее значение на данном интервале принимает в начальной (левой) точке интервала (функция возрастает слева на право).
- Началу интервала соответствует значение 1. Следовательно, в точке 1 функция принимает наименьшее значение на интервале [1;7].
Ответ: 1