Задание
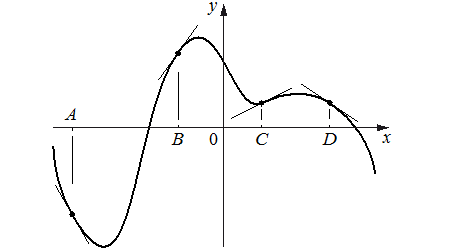
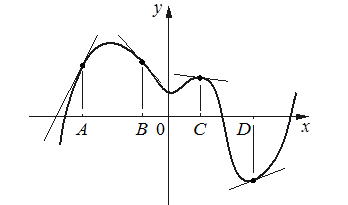
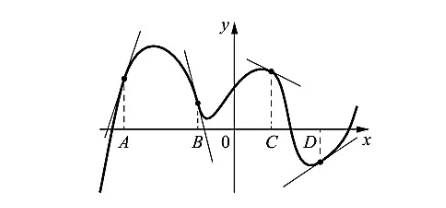
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D. В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней. В таблице для каждой точки укажите номер соответствующего значения производной.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| A | 1) -0,7 |
| B | 2) 1,4 |
| C | 3) -0,8 |
| D | 4) 0,5 |
Решение
- Для решения данной задачи будем использовать следующие правила:
— Производная функции в точки касания равна значению коэффициента касательной в этой точке.
— Если касательная образует острый угол с осью абсцисс (ось Х), то значение производной положительное. Если тупой угол, то – отрицательное. А если она параллельна оси OХ, то равна нулю.
— Чем больше угловой коэффициент касательной, тем больше касательная прижата к оси ОY (подъем касательной более крутой).
- В точках А и D касательные образует с осью Х тупой угол, значит значение их производных будет отрицательным. По графику мы видим, что касательная в точке А прижата к оси Y больше, чем в точке D (подъем касательной более крутой), а это значит и угловой коэффициент (по модулю) будет больше. Поэтому значение производных в точках будет:
А = -1,8, D = -0,7
- В точках C и B касательные образует с осью Х острый угол, значит значение их производных будет положительным. По графику мы видим, что касательная в точке B прижата к оси Y больше, чем в точке C. Поэтому значение производных в точках:
В = 1,4, С = 0,5
Ответ: 3241