Задание
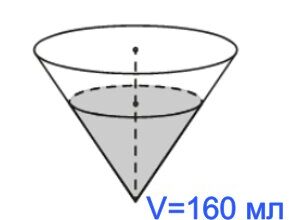
В сосуде, имеющем форму конуса, уровень жидкости достигает 2/3 высоты. Объем жидкости равен 160 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Решение
- Объем конуса равен 1/3 произведения его высоты на площадь основания, а площадь основания — это площадь круга: V=1/3*h*Socн=1/3*h*π*(D/2)2.
- Для решения данной задачи будем рассматривать объемы двух конусов:
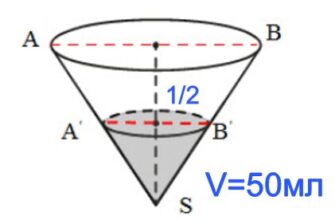
- объем конуса, у которого уровень жидкости равен 2/3 высоты – Vмен,
- объем конуса, наполненный доверху – Vбол
- Нам известно, что высота большего конуса в 3/2 раза больше высоты меньшего. Определим во сколько раз основание меньшего конуса меньше большего.
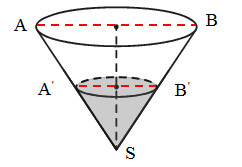
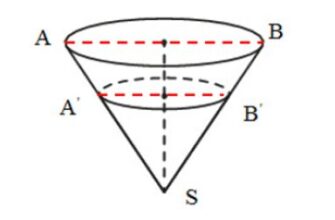
- Для удобства введем буквенные обозначения, как показано на рисунке, и рассмотрим треугольники АSВ и А‘SВ‘. Данные треугольники подобны. Из этого делаем вывод, что основание АВ больше основания А‘В‘ в 3/2 раза, так как высота треугольника АSВ в 3/2 раза больше высоты треугольника А‘SВ‘.
- АВ и А‘В‘ являются диаметрами оснований конусов. Запишем, чему равен объем большего конуса в буквенном виде:
Vбол = 1/3*h*π*(D/2)2
- Теперь запишем, чему равен объем меньшего конуса и преобразуем получившееся выражение:
Vмен = 1/3*h/(3/2)*π*(D/2/(3/2))2 = (1/3*h*π*(D/2)2)/(3/2*9/4) = Vбол/3,375 = 160 мл
- Найдем объем заполненного цилиндра, то есть объем большего конуса:
Vбол/3,375 = 160 мл
Vбол = 160*3,375 = 540 мл
- Осталось вычислить, сколько жидкости необходимо долить, чтобы заполнить сосуд доверху:
Vбол-Vмен = 540-160 = 380 мл необходимо долить.
Ответ: 380