В треугольнике ABC угол C равен 90 градусов, sinA=3/5, АС=4, СН – высота

Задание

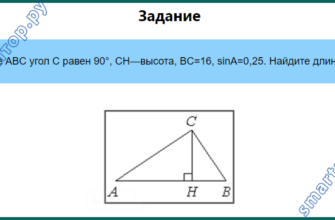
В треугольнике ABC угол C равен 90⁰, sin A = 3/5, АС = 4, СН – высота. Найдите ВН.

Решение

1. Рассмотрим треугольник АНС. Данный треугольник прямоугольный с прямым углом Н. В нём известны гипотенуза АС и синус угла А.

2. Через синус угла А найдем катет НС.

Синус – это отношение противолежащего катета к гипотенузе.

sinА = НС/АС
НС = АС*sinА
НС = 4*(3/5) = 12/5 = 2,4

3. Рассмотрим треугольник АВС с прямым углом С.

Найдем косинус угла А из основного тригонометрического тождества: sin²A + cos²A = 1

cos ²A = 1-sin²A = 1-(3/5)² = 1-9/25 = 16/25
cosА = 4/5

4. Из определения косинуса найдем гипотенузу АВ.

Косинус – это отношение прилежащего катета к гипотенузе.

cosА = АС/АВ
АВ = АС/cosA
АВ = 4/(4/5) = 5

5. С помощью теоремы Пифагора найдем катет ВС.

Теорема Пифагора: сумма квадратов катетов равна квадрату гипотенузы.

АВ² = ВС²+АС²
ВС² = АВ²-АС²
ВС² = 5²-4² = 25-16 = 9
ВС=3

6. Рассмотрим треугольник ВНС. Данный треугольник прямоугольный с прямым углом Н. В нем известны гипотенуза ВС и катет НС.

7. По теореме Пифагора найдем катет ВН:

ВС² = НС²+ВН²
ВН² = ВС²-НС²
ВН² = 3²-2,4² = 9-5,76 = 3,24
ВН=1,8

Ответ: 1,8