В треугольнике ABC угол C равен 90 градусов, СН – высота, угол А равен 60 градусов

Задание

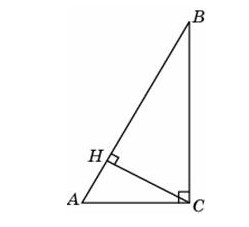
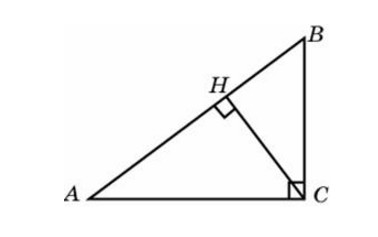
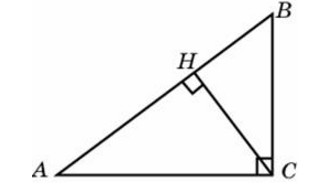
В треугольнике ABC угол C равен 90⁰, СН – высота, угол А равен 60⁰, АВ = 12. Найдите CH.

Решение

1. Рассмотрим треугольник АВС. В треугольнике АВС найдем ВС через синус угла А (синус угла – это отношение противолежащего катета к гипотенузе):

sinA =  ВС/АВ
ВС = АВ*sin A
ВС = 12*sin 60⁰
ВC = 12*(√3/2) =6√3

2. Рассмотрим треугольник ВНС.

В данном треугольнике угол В равен 30⁰ (угол В = 180⁰ – угол С – угол А = 180⁰ — 90⁰ — 60⁰ = 30⁰, так как сумма углов в любом треугольнике равна 180⁰).

3. Найдем катет ВН через косинус угла В (косинус угла – это отношение прилежащего катета к гипотенузе):

cosB = ВН/ВС
ВН = ВС*cosB
НС = 6√3*cosB 30⁰ = 6√3*(√3/2) = 9

Ответ: 9