Задача 8 (№ 1595) — Столб подпирает детскую горку посередине

Условие

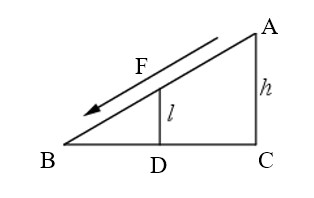
Столб подпирает детскую горку посередине. Найдите высоту l этого столба, если высота горки равна 3,4 м. Ответ дайте в метрах.

Решение

Для нахождения высоты столба рассмотрим треугольники АВС и FBD. FD = L (искомая высота), АС = h.
Данные треугольники являются подобными по трем углам.
Из подобия следует:

ВС/ВD = AC/FD

Нам известно, что столб подпирает горку посередине, то есть ВС/ВD = 2. Тогда получаем

2 = AC/FD

FD = AC/2

FD = 3,4/2

FD = 1,7

1,7 м – высота столба.

Ответ: 1,7

Задача 8 (№ 1594) — Столб подпирает детскую горку посередине

Условие

Столб подпирает детскую горку посередине. Найдите высоту l этого столба, если высота горки равна 3,2 м. Ответ дайте в метрах.

Решение

Для нахождения высоты столба рассмотрим треугольники АВС и FBD. FD = L (искомая высота), АС = h.
Данные треугольники являются подобными по трем углам.
Из подобия следует:

ВС/ВD = AC/FD

Нам известно, что столб подпирает горку посередине, то есть ВС/ВD = 2. Тогда получаем

2 = AC/FD

FD = AC/2

FD = 3,2/2

FD = 1,6

1,6 м – высота столба.

Ответ: 1,6

Задача 8 (№ 1593) — Столб подпирает детскую горку посередине

Условие

Столб подпирает детскую горку посередине. Найдите высоту l этого столба, если высота горки равна 2,8 м. Ответ дайте в метрах.

Решение

Для нахождения высоты столба рассмотрим треугольники АВС и FBD. FD = L (искомая высота), АС = h.
Данные треугольники являются подобными по трем углам.
Из подобия следует:

ВС/ВD = AC/FD

Нам известно, что столб подпирает горку посередине, то есть ВС/ВD = 2. Тогда получаем

2 = AC/FD

FD = AC/2

FD = 2,8/2

FD = 1,4

1,4 м – высота столба.

Ответ: 1,4

Задача 8 (№ 1592) — Столб подпирает детскую горку посередине

Условие

Столб подпирает детскую горку посередине. Найдите высоту l этого столба, если высота горки равна 2,5 м. Ответ дайте в метрах.

Решение

Для нахождения высоты столба рассмотрим треугольники АВС и FBD. FD = L (искомая высота), АС = h.
Данные треугольники являются подобными по трем углам.
Из подобия следует:

ВС/ВD = AC/FD

Нам известно, что столб подпирает горку посередине, то есть ВС/ВD = 2. Тогда получаем

2 = AC/FD

FD = AC/2

FD = 2,5/2

FD = 1,25

1,25 м – высота столба.

Ответ: 1,25

Задача 8 (№ 1591) — Столб подпирает детскую горку посередине

Условие

Столб подпирает детскую горку посередине. Найдите высоту l этого столба, если высота горки равна 2,2 м. Ответ дайте в метрах.

Решение

Для нахождения высоты столба рассмотрим треугольники АВС и FBD. FD = L (искомая высота), АС = h.
Данные треугольники являются подобными по трем углам.
Из подобия следует:

ВС/ВD = AC/FD

Нам известно, что столб подпирает горку посередине, то есть ВС/ВD = 2. Тогда получаем

2 = AC/FD

FD = AC/2

FD = 2,2/2

FD = 1,1

1,1 м – высота столба.

Ответ: 1,1

Задача 8 (№ 1590) — Столб подпирает детскую горку посередине

Условие

Столб подпирает детскую горку посередине. Найдите высоту l этого столба, если высота горки равна 4,2 м. Ответ дайте в метрах.

Решение

Для нахождения высоты столба рассмотрим треугольники АВС и FBD. FD = L (искомая высота), АС = h.
Данные треугольники являются подобными по трем углам.
Из подобия следует:

ВС/ВD = AC/FD

Нам известно, что столб подпирает горку посередине, то есть ВС/ВD = 2. Тогда получаем

2 = AC/FD

FD = AC/2

FD = 4,2/2

FD = 2,1

2,1 м – высота столба.

Ответ: 2,1

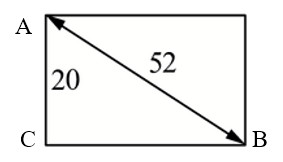
Задача 8 (№ 1580) — Диагональ прямоугольного телевизионного экрана равна 52 дюйма

Условие

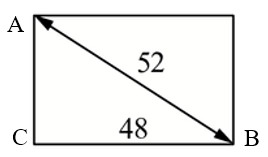
Диагональ прямоугольного телевизионного экрана равна 52 дюйма, а высота экрана – 20 дюймам. Найдите ширину экрана. Ответ дайте в дюймах.

Решение

Для нахождения ширины рассмотрим прямоугольный треугольник (для удобства назовем его АВС).
Катет СВ в данном треугольнике и есть искомая ширина телевизионного экрана.
Найдем ВС по теореме Пифагора:

АВ² = АС² + СВ²

ВС² = АВ² — АС²

ВС² = 50² — 30² = (52 – 20)(52 + 20) = 32 · 72 = 2304

ВС = 48

48 дюймов – ширина экрана.

Ответ: 48

Задача 8 (№ 1579) — Диагональ прямоугольного телевизионного экрана равна 52 дюймов

Условие

Диагональ прямоугольного телевизионного экрана равна 52 дюймов, а ширина экрана – 48 дюймам. Найдите высоту экрана. Ответ дайте в дюймах.

Решение

Для нахождения ширины рассмотрим прямоугольный треугольник (для удобства назовем его АВС).
Катет АС в данном треугольнике и есть искомая высота телевизионного экрана.
Найдем АС по теореме Пифагора:

АВ² = АС² + СВ²

АС² = АВ² — АС²

АС² = 52² — 48² = (52 – 48)(52 + 48) = 4 · 100 = 400

АС = 20

20 дюймов – высота экрана.

Ответ: 20

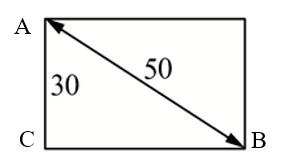
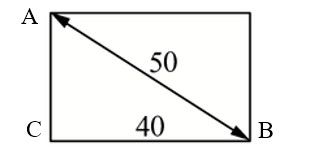
Задача 8 (№ 1578) — Диагональ прямоугольного телевизионного экрана равна 50 дюймов

Условие

Диагональ прямоугольного телевизионного экрана равна 50 дюймов, а высота экрана – 30 дюймам. Найдите ширину экрана. Ответ дайте в дюймах.

Решение

Для нахождения ширины рассмотрим прямоугольный треугольник (для удобства назовем его АВС).
Катет СВ в данном треугольнике и есть искомая ширина телевизионного экрана.
Найдем ВС по теореме Пифагора:

АВ² = АС² + СВ²

ВС² = АВ² — АС²

ВС² = 50² — 30² = (50 – 30)(50 + 30) = 20 · 80 = 1600

ВС = 40

40 дюймов – ширина экрана.

Ответ: 40

Задача 8 (№ 1577) — Диагональ прямоугольного телевизионного экрана равна 50 дюймов

Условие

Диагональ прямоугольного телевизионного экрана равна 50 дюймов, а ширина экрана – 40 дюймам. Найдите высоту экрана. Ответ дайте в дюймах.

Решение

Для нахождения ширины рассмотрим прямоугольный треугольник (для удобства назовем его АВС).
Катет АС в данном треугольнике и есть искомая высота телевизионного экрана.
Найдем АС по теореме Пифагора:

АВ² = АС² + СВ²

АС² = АВ² — АС²

АС² = 50² — 40² = (50 – 40)(50 + 40) = 10 · 90 = 900

АС = 30

30 дюйма – высота экрана.

Ответ: 30

smartrepetitor.ru

Решения и Ответы к задачам банка заданий ЕГЭ по математике

Архивы категории: Задание 8 (Базовый уровень)

Задача 8 (№ 1595) — Столб подпирает детскую горку посередине

Условие

Решение

Задача 8 (№ 1594) — Столб подпирает детскую горку посередине

Условие

Решение

Задача 8 (№ 1593) — Столб подпирает детскую горку посередине

Условие

Решение

Задача 8 (№ 1592) — Столб подпирает детскую горку посередине

Условие

Решение

Задача 8 (№ 1591) — Столб подпирает детскую горку посередине

Условие

Решение

Задача 8 (№ 1590) — Столб подпирает детскую горку посередине

Условие

Решение

Задача 8 (№ 1580) — Диагональ прямоугольного телевизионного экрана равна 52 дюйма

Условие

Решение

Задача 8 (№ 1579) — Диагональ прямоугольного телевизионного экрана равна 52 дюймов

Условие

Решение

Задача 8 (№ 1578) — Диагональ прямоугольного телевизионного экрана равна 50 дюймов

Условие

Решение

Задача 8 (№ 1577) — Диагональ прямоугольного телевизионного экрана равна 50 дюймов

Условие

Решение

Условие

Решение

Сохрани или поделись страничкой 999+

Условие

Решение

Сохрани или поделись страничкой 999+

Условие

Решение

Сохрани или поделись страничкой 999+

Условие

Решение

Сохрани или поделись страничкой 999+

Условие

Решение

Сохрани или поделись страничкой 999+

Условие

Решение

Сохрани или поделись страничкой 999+

Условие

Решение

Сохрани или поделись страничкой 999+

Условие

Решение

Сохрани или поделись страничкой 999+

Условие

Решение

Сохрани или поделись страничкой 999+

Условие

Решение

Сохрани или поделись страничкой 999+