Деталь имеет форму многогранника с ребрами 2, 2, 3, 3 и 4

Задание

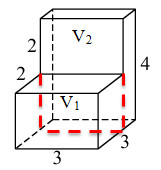
Деталь имеет форму изображенного на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины ребер в сантиметрах. Найдите объем этой детали. Ответ дайте в кубических сантиметрах.

Решение

1. Для решения данной задачи будем использовать формулу нахождения объема для прямоугольного параллелепипеда:

Объем прямоугольного параллелепипеда равен произведению его высоты на площадь основания. А площадь основания равна произведению длины на ширину: V=h*S_ocн= h*a*b.

2. Разобьём данный многогранник на два прямоугольных параллелепипеда (красной пунктирной линией показано, как можно разбить). Получили большой V₁ и маленький V₂ параллелепипеды. Найдем их объемы отдельно, а потом сложим, тем самым найдем объем всего многогранника.

V₁ = 2*2*3 = 12 см³
V₂ = 4*1*3 = 12 см³
V = V₁+V₂ = 12+12 = 24 см³ – объем исходного многогранника.

Ответ: 24