Шар вписан в цилиндр, площадь полной поверхности цилиндра равна 117

Задание

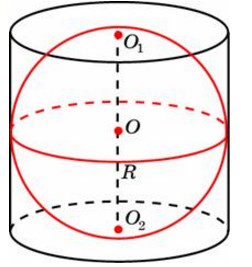
Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 117. Найдите площадь поверхности шара.

Решение

1. Площадь полной поверхности цилиндра находится по формуле: S_{целиндра}=2πr*(h+r), где h – высота цилиндра, r – радиус основания цилиндра.

2. У цилиндра, описанного около шара, высота равна диаметру шара. Тогда формула для нахождения площади поверхности цилиндра приобретает следующий вид:

S_ц = 2πr*(2r + r) = 2πr*3r = 6*π*r²
S_ц = 6πr²

3. При этом площадь поверхности шара равна: S_шара=4πr²

4. Сравнивая, формулы цилиндра и шара, получаем:

S_ш / S_ц = (4*π*r²)/(6*π*r²)
S_ш / S_ц = 4/6
S_ш = 4/6*S_ц

5. Осталось найти площадь поверхности шара:

S_ш = 4/6*S_ц  = 4/6*117 = 78

Ответ: 78