Радиус основания цилиндра равен 10, образующая равна 18

Задание

Радиус основания цилиндра равен 10, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 8. Найдите площадь этого сечения.

Решение

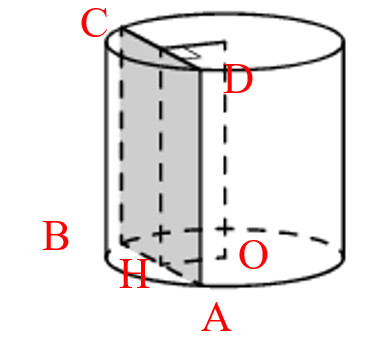
1. Для удобства введем буквенные обозначения: О – центр основания цилиндра, DA и СВ – образующие цилиндра, ОН – расстояние от оси до сечения.
2. Сечение представляет собой прямоугольник, площадь которого равна произведению двух его смежных сторон, а именно:

S = АВ*DA

DA – образующая цилиндра, следовательно DA = 18,

3. Найдем АВ. Для этого рассмотрим треугольник ОНА. Данный треугольник прямоугольный (с прямым углом Н). Так же в треугольнике известны катет ОН = 8 и гипотенуза OA = 10 (ОА – радиус основания).

По теореме Пифагора найдем катет, АН:

АН² = ОА²-ОН² = 10²-8² = 36

АН=6

4. АВ = АН+ВН, так как АН=ВН=6, то

АВ = 6+6 = 12

5. Осталось найти площадь сечения:

S = АВ*DA = 12*18 = 216 – площадь сечения

Ответ: 216