К правильной треугольной призме со стороной 1 приклеили треугольную пирамиду

Задание

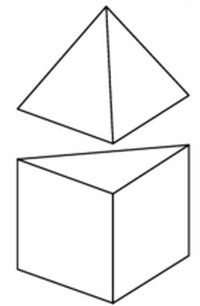
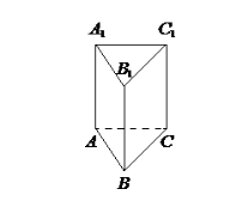
К правильной треугольной призме с ребром 1 приклеили правильную треугольную пирамиду с ребром 1 так, что основания совпали. Сколько рёбер у получившегося многогранника (невидимые ребра на рисунке не изображены)?

Решение

1. Ребро – отрезок, соединяющий две вершины многогранника.
2. Правильная треугольная пирамида имеет 6 рёбер.
3. У правильной треугольной призмы – 9 рёбер.
4. Итого, у правильной треугольной пирамиды и призмы всего 6 + 9 = 15 рёбер.
5. При приклеивании правильной треугольной пирамиды к правильной треугольной призме 3 ребра основания пирамиды и 3 ребра верхней грани призмы, к которой приклеивается пирамида, объединяются. Поэтому получившийся многогранник имеет 15 – 3 = 12 рёбер.

Ответ: 12