Задание 8 (Базовый уровень)
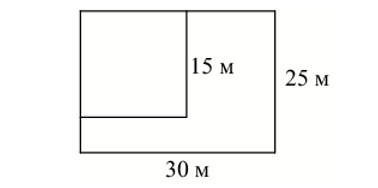
Условие Данный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров. Хозяин огородил на участке квадратный вольер со стороной 15 м (см.рис.). Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах. Решение Найдем общую площадь участка S1: S1 = 25 x 30 = 750 м2 Найдем площадь вольера S2: S2 = 15 […]
Условие Данный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров. Хозяин планирует обнести его изгородью и отгородить такой же изгородью квадратный участок со стороной 15м (см.рис.). Найдите суммарную длину изгороди в метрах. Решение Для нахождения длины изгороди находим периметр внешнего прямоугольника + длину внутренней изгороди: L = 2·(25 + 30) + 15 […]
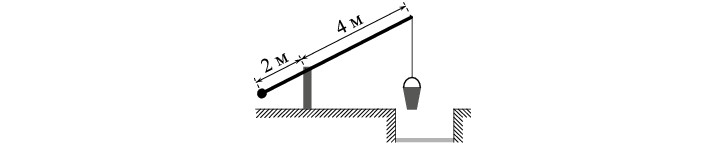
На рисунке изображен колодец с «журавлем». Короткое плечо имеет длину 2 м, а длинное плечо – 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимается на 1,5 м?
Ответ: 3.
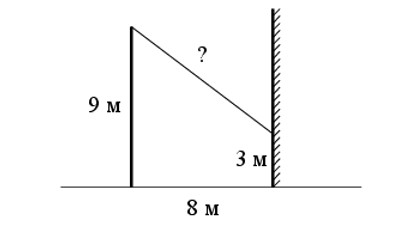
От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рис.). Расстояние от дома до столба 8 м. Найдите длину провода. Ответ дайте в метрах.
Ответ: 10.
Пол комнаты, имеющей форму прямоугольника со сторонами 4м и 9м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?
Ответ: 1440
Масштаб карты такой, что в одном сантиметре 2,5 км. Чему равно расстояние между городами А и В (в км), если на карте оно составляет 12 см?
Ответ: 30
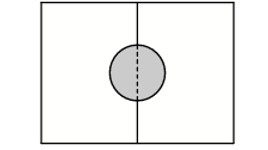
Два садовода, имеющие прямоугольные участки размерами 20 м на 30 м с общей границей, договорились и сделали общий круглый пруд площадью 140 квадратных метров (см. чертёж), причем граница участков проходит точно через центр пруда. Какова площадь (в квадратных метрах) оставшейся части участка каждого садовода?
Ответ: 530.
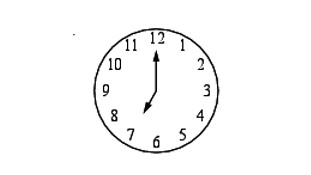
Какой наименьший угол (в градусах) образуют минутная и часовая стрелка часов в 7:00?
Ответ: 150°.
Условие Колесо имеет 15 спиц. Углы между соседними спицами равны. Найдите величину наименьшего угла (в градусах), который образует две соседние спицы. Решение Колесо образует угол, равный 360°. Разделим 360° на 15 спиц, тем самым узнаем, чему равен угол между соседними спицами: 360° : 15 = 24° — угол между соседними спицами. Ответ: 24°
План местности разбит на клетки. Каждая клетка обозначает квадрат 1м х 1м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
Ответ: 12