Объем конуса равен 500, точка делит высоту конуса в отношение 1:4

Задание

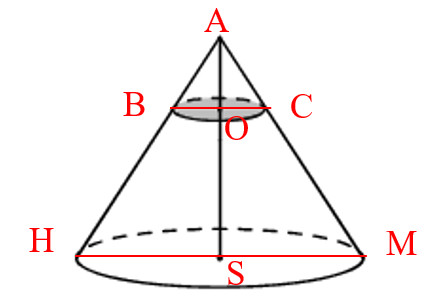
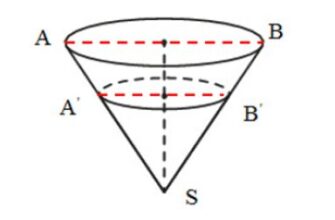
Объем конуса равен 500. Через точку, делящую высоту конуса в отношение 1:4, считая от вершины, проведена плоскость, параллельная основанию. Найдите объем конуса, отсекаемого от данного конуса, проведенной плоскостью.

Решение:

1. Объем конуса равен одной трети произведения площади его основания на высоту. Основанием конуса является круг, тогда объем конуса равен:

V = 1/3*S_{основания}*h =1/3*π*D²/4*h

2. Для удобства введем буквенные обозначения (так как представлено на рисунке).
3. Треугольники АВС и АНМ – подобны по трем углам. Из подобия треугольников следует:

ВС:НМ = AO:AS = 1:5 (из условия AO:OS = 1:4), получаем

НМ = 5*ВС
AS = 5*AO

4. Объём изначального конуса равен:

V₁ = 1/3*π*D²/4*h = 1/3*π*НМ²*АS = 1/3*π*(5*BC)²*(5*AO) = 500

5. Объём второго конуса (отсекаемого от исходного) равен:

V₂ = 1/3*π*D²/4*h = 1/3*π*ВС²*AO

6. Определим, во сколько раз объем изначального конуса больше объема отсекаемого. Для этого разделим объем первого конуса на объем второго:

V₁/V₂ = (1/3*π*(5*BC)²*(5*AO)):(1/3*π*ВС²*AO) = 125

В 125 раз объем изначального конуса больше объема отсекаемого.

7. Осталось найти объем конуса, отсекаемого от исходного конуса, проведенной плоскостью:

V₂ = V₁/125 = 500/125 = 4

4 – объем конуса, отсекаемого от исходного конуса.

Ответ: 4