Задача 16 (№ 6347) — Объем конуса равен 27

Условие:

Объем конуса равен 27. Через точку, делящую высоту конуса в отношение 1 : 2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объем конуса, отсекаемого от данного конуса, проведенной плоскостью.

Решение:

1. Объем конуса равен одной трети произведения площади его основания на высоту. Основанием конуса является круг, тогда объем конуса равен:

V = 1/3 S_{основания} · h =1/3 πD²/4 · h

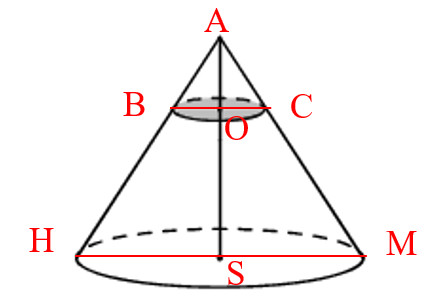
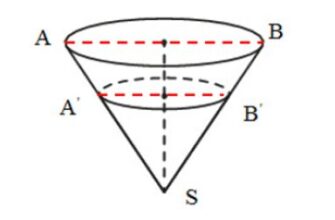
2. Для удобства введем буквенные обозначения (так как представлено на рисунке).
3. Треугольники АВС и АНМ – подобны по трем углам. Из подобия треугольников следует:

ВС : НМ = AO : AS = 1 : 3 (по условию), получаем

НМ = 3ВС

AS = 3AO

4. Тогда объём изначального конуса равен:

V₁ = 1/3 πD²/4 · h = 1/3 π · НМ² · АS =1/3 π · (3BC)² · (3AO) = 27

5. Объём второго конуса (отсекаемого от исходного) равен:

V₂ = 1/3 πD²/4 · h = 1/3 π · ВС² · AO

6. Определим, во сколько раз объем изначального конуса больше объема отсекаемого. Для этого разделим объем первого конуса на объем второго:

V₁ / V₂ = (1/3 π · (3BC)² · (3AO))  / (1/3 π · ВС² · AO) = в 27 раза объем изначального конуса больше объема отсекаемого.

7. Осталось найти объем конуса, отсекаемого от исходного конуса, проведенной плоскостью:

V₂ = V₁ / 27 = 27 / 27 = 1 – объем конуса, отсекаемого от исходного конуса.

Ответ: 1