Прямоугольник разбит на четыре меньших прямоугольника, их площади равны 12, 18, 30

Задание

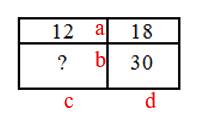
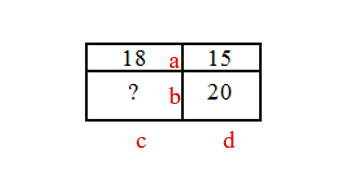
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Площади трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 12, 18 и 30. Найдите площадь четвёртого прямоугольника.

Решение

1. Для удобства введем буквенное обозначение сторон прямоугольника:

2. Мы знаем, что площадь прямоугольника равна произведению его ширины на длину S = a * b

Найдем сторону с:

S1 = a * c = 12
S2 = a * d = 18
S1 / S2 = (a * c) / (a * d) = 12 / 18
(a * c) / (a * d) = 12 / 18
c / d = 12 / 18
c = 12d / 18 = 2/3 d

Найдем сторону b:

S2 = a * d = 18
S3 = b * d = 30
S2 / S3 = (a * d) / (b * d) = 18 / 30
(a * d) / (b * d) = 18 / 30
a / b = 18 / 30
b = 30a / 18 = 5/3 a

Тогда площадь четвертого треугольника равна:
S = b * c = 5/3 a * 2/3 d = 10/9 a * d = 10/9 * 18 = 10 * 2 = 20

Ответ: 20