Стороны пирамиды равны 14, боковые ребра равны 25

Задание

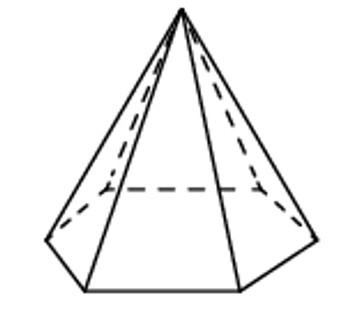
Стороны основания правильной шестиугольной пирамиды равны 14, боковые ребра равны 25. Найдите площадь боковой поверхности этой пирамиды.

Решение:

1. Чтобы найти площадь боковой поверхности правильной шестиугольной пирамиды, найдем площадь одной из её шести граней.
2. Гранью пирамиды является треугольник, площадь которого можно найти по формуле Герона:

S = , где р – полупериметр треугольника, а, b, с – длины сторон треугольника.

p = (a+b+c)/2 = (14+25+25)/2 = 32

S_гр =  = 168

3. Осталось найти площадь боковой поверхности пирамиды. Для этого площадь одной грани умножим на 6 (так как у пирамиды 6 граней):

S = S_гр·6 = 168·6 = 1008

Ответ:  1008