Первая кружка в 4,5 раза выше  второй, а вторая в 1,5 шире

Задание

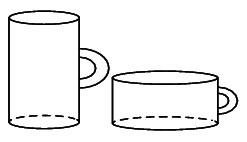
Две кружки имеют форму цилиндра. Первая кружка в четыре с половиной раза выше  второй, а вторая в полтора шире первой. Во сколько раз объём первой кружки больше объёма второй?

Решение

1. Для решения данной задачи необходимо знать формулу для нахождения объема цилиндра (так как две кружки имеют форму цилиндра):

Объем цилиндра равен произведению его высоты на площадь основания (основание цилиндра – это круг, поэтому площадь основания равна площади круга):

V = h*S_осн = h*π*r² = h*π*D²/4

2. Найдем объем второй кружки (которая ниже):

V₂ = h·π·D²/4

3. Найдем объем первой кружки:

V₁ = 4,5h·π·(2/3D)²/4

4. Осталось найти, во сколько объём первой кружки боьше объёма второй:

V₁/V₂ = 4,5*h·π·(2/3D)²/4 : (h*π*D²/4) = 2

В 2 раз объём первой кружки больше объёма второй.

Ответ: 2