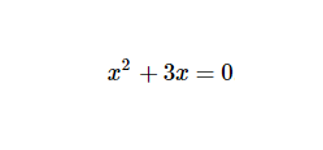Камни пролетали над стеной 14 м на высоте не менее 1 метра

Задание

Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полёта камня описывается формулой  y = ax²+bx, где a = -1/100 м^-1,  b = 4/5 — постоянные параметры, x (м) — смещение камня по горизонтали, y (м) — высота камня над землёй. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 14 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?

Решение

1. Определим высоту, на которой должен пролететь камень. Эта высота равна высоте стены плюс 1 метр:

14+1 = 15 – необходимая высота полета камня над землей (обозначим как у)

2. Подставим найденную высоту и все известные параметры в формулу y = ax²+bx, тем самым найдем наибольшее расстояние от машины до стены, при котором камень пролетит над стеной на высоте не менее 1 метр:

15 = -1/100*x²+4/5*x
1/100х²-4/5х+15 = 0

Разделим каждое слагаемое на 1/100, получим:

х²-80+1500 = 0

Решим получившееся квадратное уравнение с помощью теоремы Виета:

х₁ = 50 м
х₂ = 30 м

3. Нам нужно найти наибольшее расстояние, поэтому

х = 50 м — наибольшее расстояние от машины до стены, при котором камень пролетит над стеной на высоте не менее 1 метр.

Ответ: 50