Найдите диагональ, если площадь поверхности куба равна 18

Площадь поверхности куба равна 18. Найдите его диагональ.

Решение

1. Грань куба представляет собой квадрат. Поэтому площадь всей поверхности куба равна произведению площади одной грани на количество граней, то есть на 6: S=S_грани*6.
2. Найдем площадь одной грани:

S_грани = S/6 = 18/6 = 3 – площадь одной грани.

3. В свою очередь мы понимаем, что площадь грани равна произведению её ширины на длину. У квадрата ширина равна длине. На основе этого найдем длину ребра куба (длина ребра есть и длина и ширина грани):

S_грани = a² = 3

a = √3 – длина ребра куба.

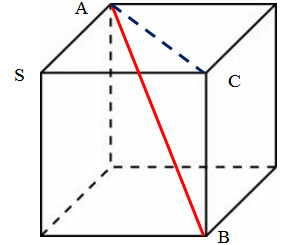
4. Проведем диагональ (красная линия).
5. Введем буквенные обозначения для удобства.
6. Найдем сперва гипотенузу АС из треугольника АСS по теореме Пифагора:

АС² = АS²+SС² = (√3)²+(√3)² = 6

7. Теперь по теореме Пифагора найдем гипотенузу АВ треугольника АСВ. Данная гипотеза и есть искомая диагональ куба:

АВ² = АС²+BС² = 6+(√3)² = 6+3 = 9

АВ = 3 – диагональ куба.

Ответ: 3