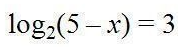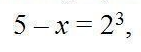6 способов решения логарифмических уравнений

Решение уравнений, основанных на определении логарифма

По определению логарифма

откуда x = -3
x = -3 это корень уравнения

Ответ: x = -3

Замена переменных в уравнениях

Две основные идеи решения логарифмических уравнений:

1) Приведение уравнения к виду

с последующим потенцированием.

2) Замена неизвестных вида

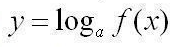
с предшествующим преобразованием уравнения к удобному для этой замены виду.

Решение уравнений с помощью потенцирования

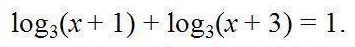
Потенцируя, имеем:

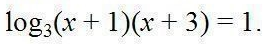
Учитывая область определения получаем систему:

Откуда x₁ = 0, x₂ = -4
Так как x > -1, то корень x₂ = -4 — посторонний

Ответ: x = 0

Применение основного логарифмического тождества

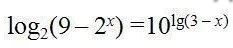
Область определения уравнения

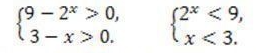
откуда x < 3. Применив в правой части основное логарифмическое тождество, получим:

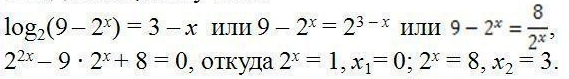
Так как x < 3, то x₂ = 3 — посторонний корень.

Ответ: x = 0

Логарифмирование

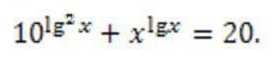
Область определения уравнения задается условиями

Прологарифмируем обе части уравнения по основанию 10, предварительно упростив его

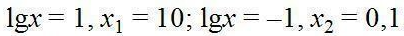
Оба корня удовлетворяют ограничениям x>0, x<>1

Ответ: x₁ = 10, x₂ = 0,1

Замена переменной

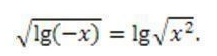
Так как -x>0, то есть x<0 и

то данное уравнение можно записать в виде

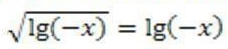
Пусть

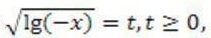
тогда получаем t = t², t(t-1) = 0, откуда t₁=0, t₂=1.

Значит

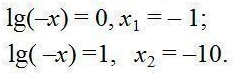
Ответ: x₁= -1, x₂= -10

Переход к другому основанию

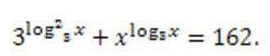
Запишем уравнение в виде

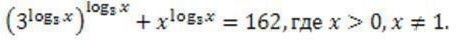
Далее имеем

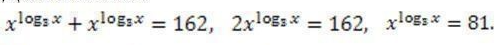
Прологарифмировав обе части уравнения по основанию 3, получим:

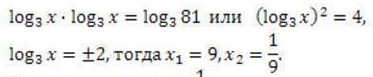
Ответ: x₁ = 9, x₂ = 1/9