Задание 4 (Профильный уровень)

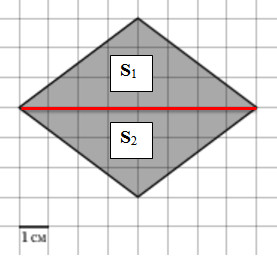
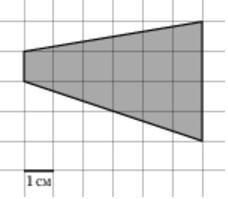
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см. Ответ дайте в квадратных сантиметрах. Ответ: 24

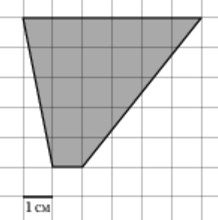
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см. Ответ дайте в квадратных сантиметрах. Ответ: 24,5

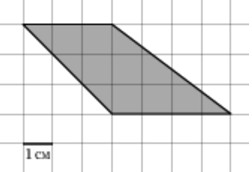
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см. Ответ дайте в квадратных сантиметрах. Ответ: 12,5

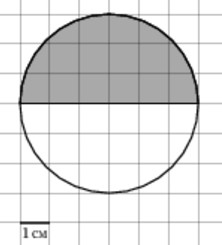
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). В ответе запишите S/π. Ответ: 4,5

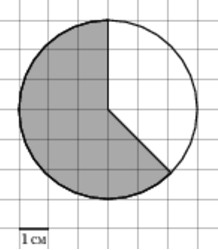
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). В ответе запишите S/π. Ответ: 5,625

Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). В ответе запишите S/π. Ответ: 8

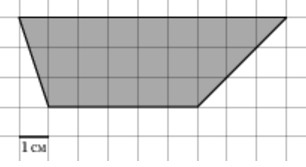
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. Ответ: 21

Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. Ответ: 15

Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. Ответ: 10,5

Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. Ответ: 10,5