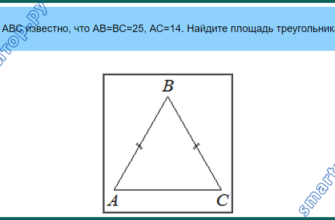
В треугольнике АВС известно, что АВ=ВС=25, АС=14. Найдите площадь треугольника AВC.
Ответ: 168.
1.4к.
Площадь треугольника вычисляется по формуле S = 1/2*bc*sinα, где b и c – стороны треугольника, а α –
913
Площадь треугольника можно вычислить по формуле S = abc/(4R), где а, b и c – стороны треугольника, а
6.8к.
Площадь треугольника можно вычислить по формуле S = abc / (4R), где а, b и c – стороны треугольника
3.6к.
Площадь треугольника можно вычислить по формуле S = abc / (4R), где а, b и c – стороны треугольника
6.9к.
Площадь треугольника вычисляется по формуле S=1/2bc*sinα, где, b и с – две стороны треугольника, а α
2.1к.
Площадь треугольника можно вычислить по формуле S = abc / (4R), где a, b и с – стороны треугольника
17.1к.
План местности разбит на клетки. Каждая клетка обозначает квадрат 1м х 1м. Найдите площадь участка, выделенного на плане.
22.2к.