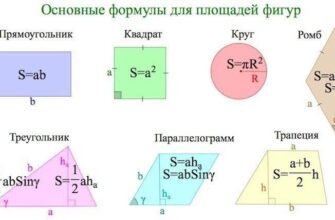
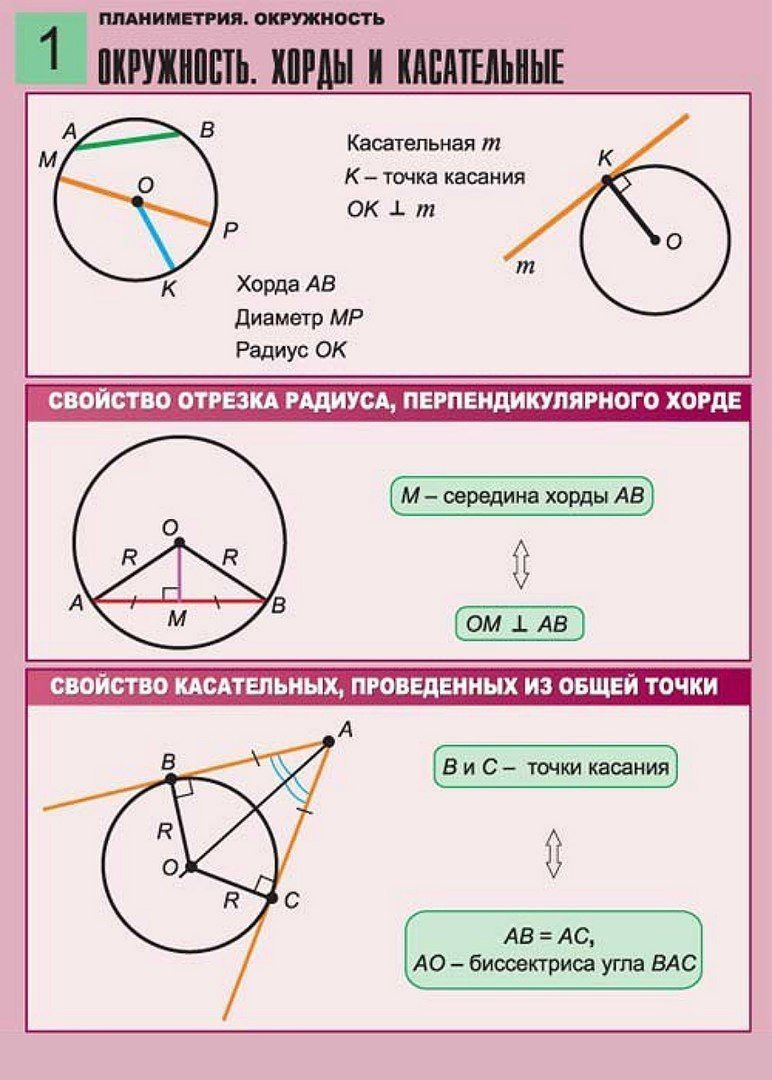
На портале smartrepetitor.ru представлена теория и практика решения задач по математике разного уровня сложности. Для продуктивной работы воспользуйтесь поиском на сайте, а также главным меню или меню по категориям.
Если нашли ошибку, или у вас появились вопросы, то напишите нам на почту smartrepetitor@yandex.ru