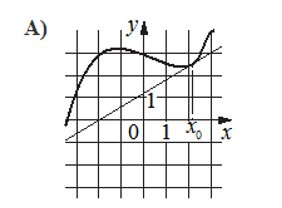Задание
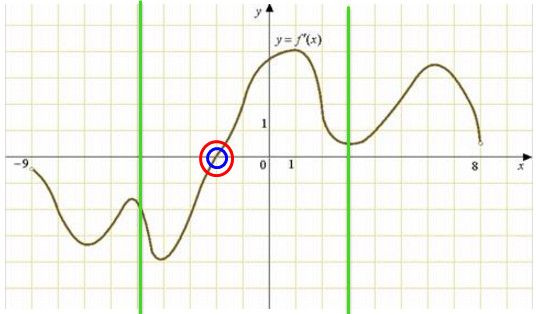
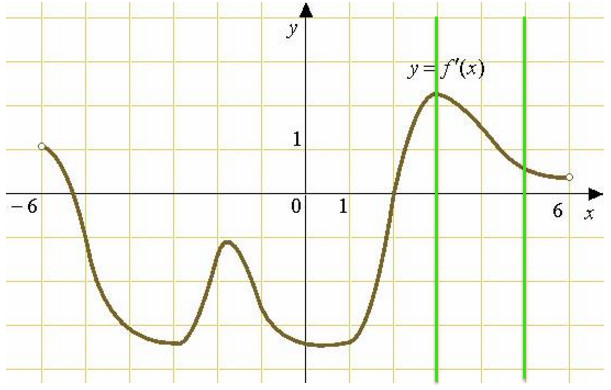
На рисунке изображён график y=f'(x) производной функции f(x), определенной на интервале (-9;8). В какой точке отрезка [-5;3] функция f(x) принимает наименьшее значение?
Решение
- Обратим внимание на то, что на рисунке изображен график производной функции. Покажем рабочий интервал [-5;3]вертикальными зелеными линиями.
- Мы знаем, что в точках экстремума производная функции равна 0. Получается, что точки экстремума можно спокойно определить по графику производной функции. Покажем данные точки синим цветом.
Экстремумы – это максимальное (максимум) или минимальное (минимум) значения функции.
- В задаче необходимо найти минимальное значение функции, то есть минимум. Минимум – это наименьшее значение функции. В точке минимума функция меняется с убывания на возрастание.
- У нас дан график производной функции. Мы знаем, если производная функции положительна, то функция возрастает, если производная функции отрицательна – функция убывает.
- На основе выше сказанного делаем вывод, что в точке минимума производная меняет свой знак с минуса на плюс. Обведем красным цветом все точки, которые подходят данному условию. Получили, что в точке -2 функция принимает наименьшее значение.
Ответ: -2