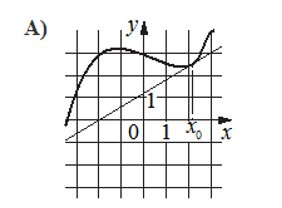Задание
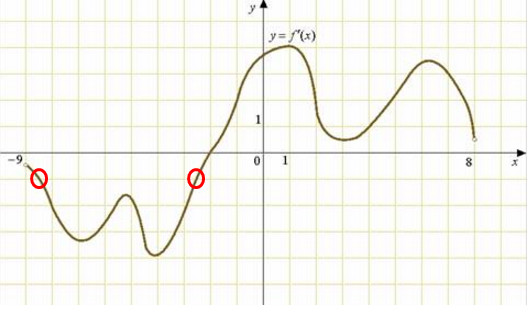
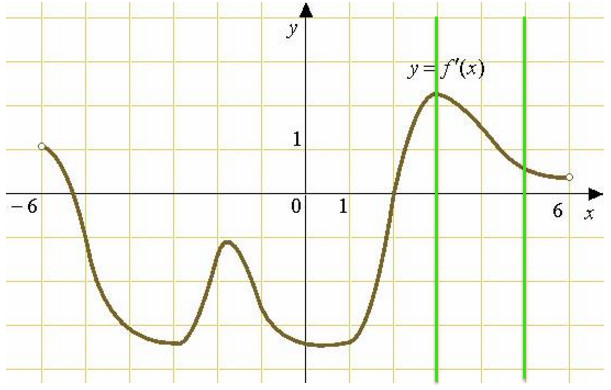
На рисунке изображен график y=f'(x) — производной функции f(x), определенной на интервале (-9;8). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=-x+8 или совпадает с ней?
Решение
- Обратим внимание на то, что на рисунке изображен график производной функции.
- Производная функции в точке касания равна угловому коэффициенту касательной.
- Угловой коэффициент прямой – это коэффициент, который стоит перед х, если уравнение прямой записать в виде y = kx + b, то k – угловой коэффициент.
- У параллельных прямых угловые коэффициенты равны.
- Из всего выше сказанного, делаем вывод, что нам необходимо посчитать точки, в которых производная функции равна угловому коэффициенту касательной, а именно -1 (угловой коэффициент касательной равен -1).
- То есть, мы считаем точки, в которых у = -1, так как значение производной функции смотрим по оси у (данные точки выделены красным)
- Получили 2 точки, в которых касательная к графику функции параллельна прямой у = -х + 8.
Ответ: 2