Задание 9 (Профильный уровень)
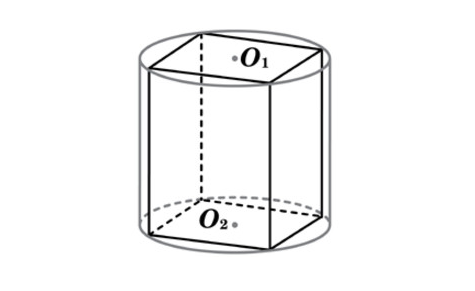
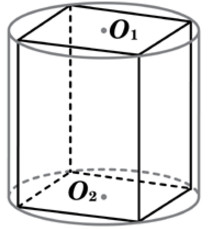
В основании прямой призмы лежит квадрат со стороной 7. Боковые ребра призмы равны 2/π. Найдите объём цилиндра, описанного около этой призмы.
Ответ: 49.
В основании прямой призмы лежит квадрат со стороной 9. Боковые ребра призмы равны 1/π. Найдите объём цилиндра, описанного около этой призмы.
Ответ: 81
В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра призмы равны 2/π. Найдите объём цилиндра, описанного около этой призмы.
Ответ: 4.
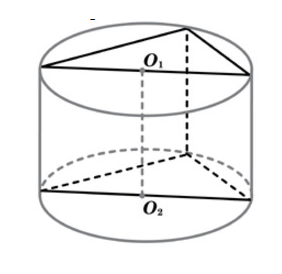
В основании прямой призмы лежит прямоугольный треугольник с катетами 9 и 3. Боковые ребра призмы равны 5/π. Найдите объём цилиндра, описанного около этой призмы.
В основании прямой призмы лежит прямоугольный треугольник с катетами 4 и 1. Боковые ребра призмы равны 2/π. Найдите объём цилиндра, описанного около этой призмы.
Ответ: 8,5.
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра призмы равны 5/π. Найдите объём цилиндра, описанного около этой призмы.
Ответ: 125.
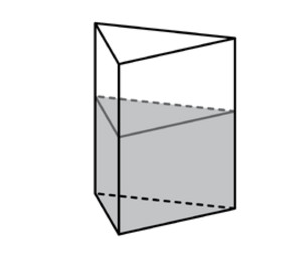
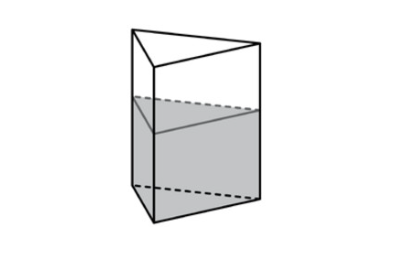
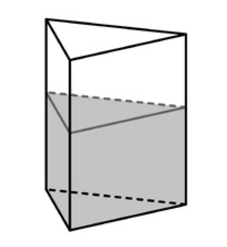
В сосуд, имеющий форму правильной треугольной призмы, налили 1000 см3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 20 см до отметки 22 см. Чему равен объем детали? Ответ выразите в см3.
Ответ: 100
В сосуд, имеющий форму правильной треугольной призмы, налили 1600 см3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 28 см. Чему равен объем детали? Ответ выразите в см3.
Ответ: 192.
В сосуд, имеющий форму правильной треугольной призмы, налили 1200 см3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 24 см до отметки 26 см. Чему равен объем детали? Ответ выразите в см3.
Ответ: 100
В сосуд, имеющий форму правильной треугольной призмы, налили 1300 см3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 20 см до отметки 23 см. Чему равен объем детали? Ответ выразите в см3.
Ответ: 195.