Задание 8 (Базовый уровень)
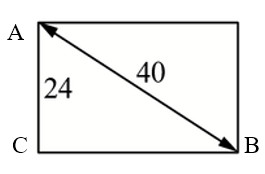
Диагональ прямоугольного телевизионного экрана равна 40 дюймов, а высота экрана – 24 дюймам. Найдите ширину экрана. Ответ дайте в дюймах.
Ответ: 32.
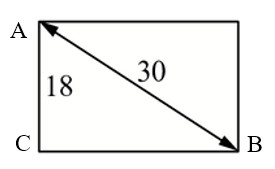
Диагональ прямоугольного телевизионного экрана равна 30 дюймов, а высота экрана – 18 дюймам. Найдите ширину экрана. Ответ дайте в дюймах.
Ответ: 24.
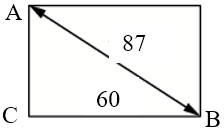
Диагональ прямоугольного телевизионного экрана равна 87 см, а ширина экрана – 60 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
Ответ: 63.
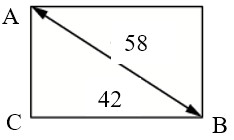
Диагональ прямоугольного телевизионного экрана равна 58 см, а ширина экрана – 42 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
Ответ: 40.
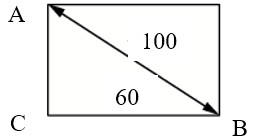
Диагональ прямоугольного телевизионного экрана равна 100 см, а ширина экрана – 60 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
Ответ: 80.
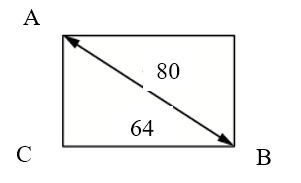
Диагональ прямоугольного телевизионного экрана равна 80 см, а ширина экрана – 64 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
Ответ: 48
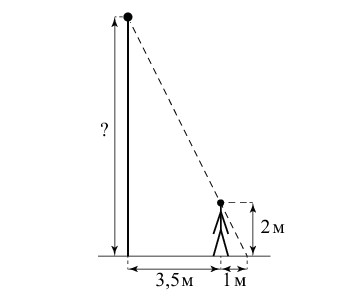
Человек, рост которого равен 2 м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
Ответ: 9
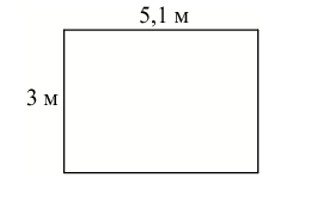
На плане указано, что прямоугольная комната имеет площадь 15,2 кв.м. Точные измерения показали, что ширина комнаты равна 3 м, а длина 5,1 м. На сколько квадратных метров площадь комнаты отличается от значений, указанных на плане?
Ответ: 0,1.
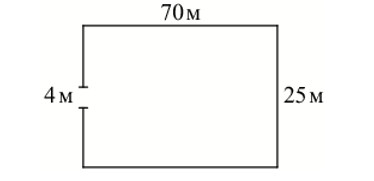
Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 25 м и 70 м. Найдите длину забора (в метрах), которым можно огородить участок, предусмотрев проезд шириной 4 м.
Ответ: 186.
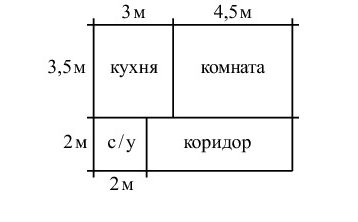
Квартира состоит из комнаты, кухни, коридора и санузла (см. чертёж). Кухня имеет размеры 3м х 3,5м, санузел – 2м х 2м, длина комнаты 4,5м. Найдите площадь коридора (в квадратных метрах).
Ответ: 11